Precision annoy.AnnoyIndex with examples#

An example showing the AnnoyIndex class.

from __future__ import print_function

import random; random.seed(0)
import time

# from annoy import AnnoyIndex
# from scikitplot.annoy import AnnoyIndex
from scikitplot.annoy import Index as AnnoyIndex

try:
    from tqdm.auto import tqdm, trange
except ImportError:
    # Fallback: dummy versions that ignore all args/kwargs
    tqdm = lambda iterable, *args, **kwargs: iterable
    trange = lambda n, *args, **kwargs: range(n)

n, f = 1_000_000, 100 # 100~2.5GB

n, f = 100_000, 100  # 100~0.25GB 256~0.6GB


idx = AnnoyIndex(
    f=f,
    metric='angular',
)
idx.set_seed(0)
for i in trange(n):
    if(i % (n//10) == 0): print(f"{i} / {n} = {1.0 * i / n}")
    # v = []
    # for z in range(f):
    #     v.append(random.gauss(0, 1))
    v = [random.gauss(0, 1) for _ in range(f)]
    idx.add_item(i, v)

idx.build(2 * f)
idx.save('test.annoy')
idx.info()

/home/circleci/repo/galleries/examples/annoy/plot_precision_script.py:37: UserWarning:

seed=0 resets to Annoy's default seed


  0%|          | 0/100000 [00:00<?, ?it/s]0 / 100000 = 0.0

  2%|▏         | 1525/100000 [00:00<00:06, 15245.76it/s]
  3%|▎         | 3115/100000 [00:00<00:06, 15628.97it/s]
  5%|▍         | 4678/100000 [00:00<00:06, 15251.59it/s]
  6%|▋         | 6272/100000 [00:00<00:06, 15515.78it/s]
  8%|▊         | 7825/100000 [00:00<00:06, 15327.47it/s]
  9%|▉         | 9406/100000 [00:00<00:05, 15488.24it/s]10000 / 100000 = 0.1

 11%|█         | 10956/100000 [00:00<00:05, 15418.02it/s]
 12%|█▏        | 12499/100000 [00:00<00:05, 15404.56it/s]
 14%|█▍        | 14055/100000 [00:00<00:05, 15451.83it/s]
 16%|█▌        | 15601/100000 [00:01<00:05, 15449.01it/s]
 17%|█▋        | 17147/100000 [00:01<00:05, 15409.52it/s]
 19%|█▊        | 18690/100000 [00:01<00:05, 15412.50it/s]20000 / 100000 = 0.2

 20%|██        | 20292/100000 [00:01<00:05, 15594.92it/s]
 22%|██▏       | 21852/100000 [00:01<00:05, 15526.58it/s]
 23%|██▎       | 23405/100000 [00:01<00:04, 15519.22it/s]
 25%|██▌       | 25083/100000 [00:01<00:04, 15896.81it/s]
 27%|██▋       | 26673/100000 [00:01<00:04, 15508.49it/s]
 28%|██▊       | 28351/100000 [00:01<00:04, 15880.93it/s]
 30%|██▉       | 29980/100000 [00:01<00:04, 16001.71it/s]30000 / 100000 = 0.3

 32%|███▏      | 31582/100000 [00:02<00:04, 15888.59it/s]
 33%|███▎      | 33173/100000 [00:02<00:04, 15711.98it/s]
 35%|███▍      | 34746/100000 [00:02<00:04, 15463.59it/s]
 36%|███▋      | 36294/100000 [00:02<00:04, 15441.23it/s]
 38%|███▊      | 37879/100000 [00:02<00:03, 15560.55it/s]
 39%|███▉      | 39444/100000 [00:02<00:03, 15584.52it/s]40000 / 100000 = 0.4

 41%|████      | 41028/100000 [00:02<00:03, 15658.66it/s]
 43%|████▎     | 42625/100000 [00:02<00:03, 15749.57it/s]
 44%|████▍     | 44240/100000 [00:02<00:03, 15868.25it/s]
 46%|████▌     | 45828/100000 [00:02<00:03, 15546.51it/s]
 47%|████▋     | 47385/100000 [00:03<00:03, 15456.07it/s]
 49%|████▉     | 48932/100000 [00:03<00:03, 15316.94it/s]50000 / 100000 = 0.5

 50%|█████     | 50465/100000 [00:03<00:03, 15183.54it/s]
 52%|█████▏    | 52027/100000 [00:03<00:03, 15311.24it/s]
 54%|█████▎    | 53560/100000 [00:03<00:03, 15314.65it/s]
 55%|█████▌    | 55100/100000 [00:03<00:02, 15337.91it/s]
 57%|█████▋    | 56635/100000 [00:03<00:02, 15029.50it/s]
 58%|█████▊    | 58140/100000 [00:03<00:02, 14983.69it/s]
 60%|█████▉    | 59640/100000 [00:03<00:02, 14794.82it/s]60000 / 100000 = 0.6

 61%|██████    | 61121/100000 [00:03<00:02, 14676.54it/s]
 63%|██████▎   | 62595/100000 [00:04<00:02, 14694.37it/s]
 64%|██████▍   | 64149/100000 [00:04<00:02, 14943.16it/s]
 66%|██████▌   | 65645/100000 [00:04<00:02, 14393.72it/s]
 67%|██████▋   | 67244/100000 [00:04<00:02, 14854.87it/s]
 69%|██████▉   | 68811/100000 [00:04<00:02, 15092.95it/s]70000 / 100000 = 0.7

 70%|███████   | 70325/100000 [00:04<00:02, 14520.69it/s]
 72%|███████▏  | 71856/100000 [00:04<00:01, 14747.87it/s]
 73%|███████▎  | 73355/100000 [00:04<00:01, 14818.04it/s]
 75%|███████▍  | 74841/100000 [00:04<00:01, 14590.94it/s]
 76%|███████▋  | 76304/100000 [00:05<00:01, 14083.13it/s]
 78%|███████▊  | 78017/100000 [00:05<00:01, 14956.20it/s]
 80%|███████▉  | 79647/100000 [00:05<00:01, 15345.12it/s]80000 / 100000 = 0.8

 81%|████████▏ | 81274/100000 [00:05<00:01, 15616.02it/s]
 83%|████████▎ | 82841/100000 [00:05<00:01, 14910.20it/s]
 84%|████████▍ | 84342/100000 [00:05<00:01, 14458.63it/s]
 86%|████████▌ | 85978/100000 [00:05<00:00, 14998.03it/s]
 88%|████████▊ | 87604/100000 [00:05<00:00, 15359.85it/s]
 89%|████████▉ | 89148/100000 [00:05<00:00, 15175.38it/s]90000 / 100000 = 0.9

 91%|█████████ | 90848/100000 [00:05<00:00, 15706.04it/s]
 93%|█████████▎| 92520/100000 [00:06<00:00, 16002.31it/s]
 94%|█████████▍| 94163/100000 [00:06<00:00, 16128.43it/s]
 96%|█████████▌| 95848/100000 [00:06<00:00, 16342.44it/s]
 97%|█████████▋| 97485/100000 [00:06<00:00, 16150.43it/s]
 99%|█████████▉| 99103/100000 [00:06<00:00, 15864.11it/s]
100%|██████████| 100000/100000 [00:06<00:00, 15361.99it/s]

{'f': 100, 'metric': 'angular', 'n_neighbors': 5, 'on_disk_path': 'test.annoy', 'prefault': False, 'seed': None, 'verbose': None, 'schema_version': 0, 'n_items': 100000, 'n_trees': 200, 'memory_usage_byte': 270651036, 'memory_usage_mib': 258.11294174194336}

def plot(idx, y=None, **kwargs):
    import numpy as np
    import matplotlib.pyplot as plt
    import scikitplot.cexternals._annoy._plotting as utils

    single = np.zeros(idx.get_n_items(), dtype=int)
    if y is None:
        double = np.random.uniform(0, 1, idx.get_n_items()).round()

    # single vs double
    fig, ax = plt.subplots(ncols=2, figsize=(12, 5))
    alpha = kwargs.pop("alpha", 0.8)
    y2 = utils.plot_annoy_index(
        idx,
        dims = list(range(idx.f)),
        plot_kwargs={"draw_legend": False},
        ax=ax[0],
    )[0]
    utils.plot_annoy_knn_edges(
        idx,
        y2,
        k=1,
        line_kwargs={"alpha": alpha},
        ax=ax[1],
    )

# idx.unbuild()
# idx.build(10)
plot(idx)

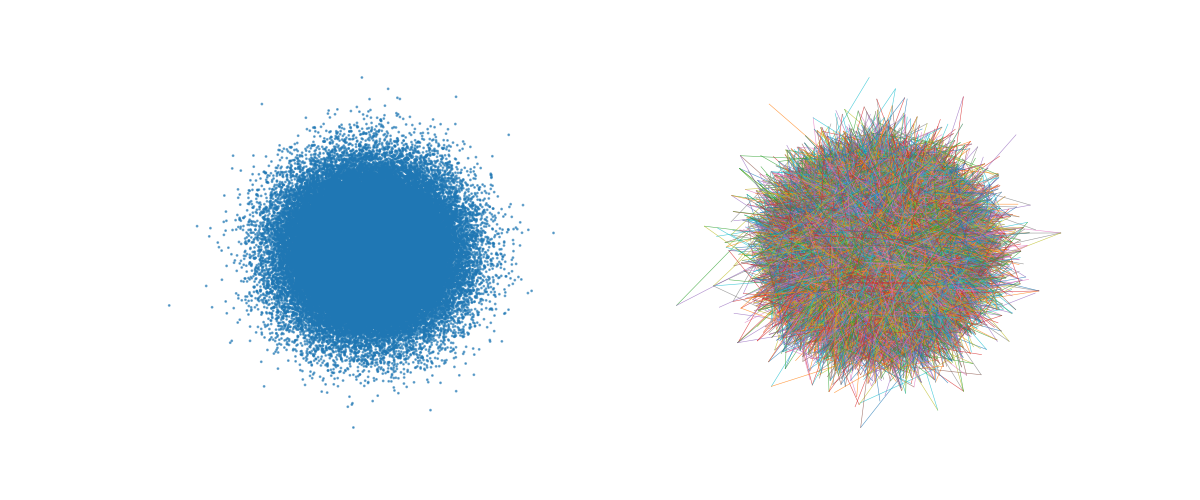
def precision(q):
  limits = [10, 100, 1_000, 10_000]
  k = 10
  prec_n = 10
  prec_sum = {}
  time_sum = {}

  for i in trange(prec_n):
      j = random.randrange(0, n)
      closest = set(q.get_nns_by_item(j, k, n))
      for limit in limits:
          t0 = time.time()
          toplist = q.get_nns_by_item(j, k, limit)
          T = time.time() - t0

          found = len(closest.intersection(toplist))
          hitrate = 1.0 * found / k
          prec_sum[limit] = prec_sum.get(limit, 0.0) + hitrate
          time_sum[limit] = time_sum.get(limit, 0.0) + T

  for limit in limits:
      print('limit: %-9d precision: %6.2f%% avg time: %.6fs'
      % (limit, 100.0 * prec_sum[limit] / (i + 1), time_sum[limit] / (i + 1)))

q = AnnoyIndex(f, 'angular')
q.set_seed(0)
q.load('test.annoy')
precision(q)

/home/circleci/repo/galleries/examples/annoy/plot_precision_script.py:111: UserWarning:

seed=0 resets to Annoy's default seed


  0%|          | 0/10 [00:00<?, ?it/s]
 70%|███████   | 7/10 [00:00<00:00, 67.72it/s]
100%|██████████| 10/10 [00:00<00:00, 68.82it/s]
limit: 10        precision:  11.00% avg time: 0.000144s
limit: 100       precision:  12.00% avg time: 0.000098s
limit: 1000      precision:  33.00% avg time: 0.000275s
limit: 10000     precision:  76.00% avg time: 0.001839s

Tags: model-type: classification model-workflow: impute plot-type: bar level: beginner purpose: showcase

Total running time of the script: (2 minutes 3.692 seconds)

Related examples