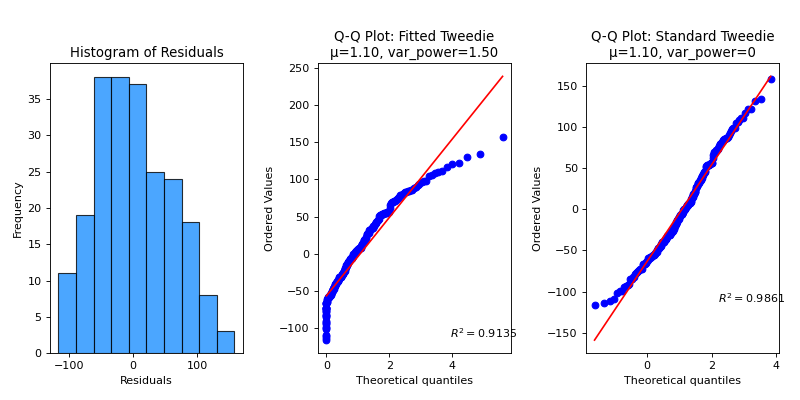
plot_residuals_distribution#

scikitplot.api.metrics.plot_residuals_distribution(y_true, y_pred, *, dist_type='normal', var_power=1.5, title='Precision-Recall AUC Curves', ax=None, fig=None, figsize=(10, 5), title_fontsize='large', text_fontsize='medium', cmap=None, show_labels=True, digits=4, **kwargs)[source]#

Plot residuals and fit various distributions to assess their goodness of fit.

Parameters:
y_truearray-like, shape (n_samples,)

Ground truth (correct) target values.

y_predarray-like, shape (n_samples,)

Estimated targets as returned by a classifier.

dist_typestr, optional, default=’normal’

Type of distribution to fit to the residuals. Options are:

  • ‘normal’: For symmetrically distributed residuals (mean μ, std σ).

  • ‘poisson’: For count-based residuals or rare events (mean λ).

  • ‘gamma’: For positive, skewed residuals with a heavy tail (shape k or α, scale θ or β).

  • ‘inverse_gaussian’: For residuals with a distribution similar to the inverse Gaussian (mean μ, scale λ).

  • ‘exponential’: For non-negative residuals with a long tail (scale λ).

  • ‘lognormal’: For positively skewed residuals with a multiplicative effect (shape σ, scale exp(μ)).

  • ‘tweedie’: For complex data including counts and continuous components.

The Tweedie distribution can model different types of data based on the variance power (var_power):

  • var_power = 0: Normal distribution (mean μ, std σ)

  • var_power = 1: Poisson distribution (mean λ)

  • 1 < var_power < 2: Compound Poisson-Gamma distribution

  • var_power = 2: Gamma distribution (shape k, scale θ)

  • var_power = 3: Inverse Gaussian distribution (mean μ, scale λ)

var_powerfloat or None
The variance power for the Tweedie distribution, applicable if dist_type='tweedie'.

  • Default is 1.5, which means Tweedie-specific plotting.

  • Example values: 1.5 for Compound Poisson-Gamma distribution, 2 for Gamma distribution.

titlestr, optional, default=’Precision-Recall AUC Curves’

Title of the generated plot.

axlist of matplotlib.axes.Axes, optional, default=None

The axis to plot the figure on. If None is passed in the current axes will be used (or generated if required). Axes like fig.add_subplot(1, 1, 1) or plt.gca()

figmatplotlib.pyplot.figure, optional, default: None

The figure to plot the Visualizer on. If None is passed in the current plot will be used (or generated if required).

Added in version 0.3.9.

figsizetuple of int, optional, default=(10, 5)

Size of the figure (width, height) in inches.

title_fontsizestr or int, optional, default=’large’

Font size for the plot title.

text_fontsizestr or int, optional, default=’medium’

Font size for the text in the plot.

cmapNone, str or matplotlib.colors.Colormap, optional, default=None

Colormap used for plotting. Options include ‘viridis’, ‘PiYG’, ‘plasma’, ‘inferno’, ‘nipy_spectral’, etc. See Matplotlib Colormap documentation for available choices.

show_labelsbool, optional, default=True

Whether to display the legend labels.

digitsint, optional, default=3

Number of digits for formatting PR AUC values in the plot.

Added in version 0.3.9.

Returns:
axmatplotlib.axes.Axes

The axes on which the plot was drawn.

Raises:
ValueError: If an unsupported distribution type is provided or if var_power is invalid.

Examples

>>> import numpy as np; np.random.seed(0)
>>> from sklearn.datasets import load_diabetes as data_regression
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import Ridge
>>> import scikitplot as skplt
>>>
>>> X, y = data_regression(return_X_y=True, as_frame=False)
>>> X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.5, random_state=0)
>>> model = Ridge(alpha=1.0).fit(X_train, y_train)
>>> y_val_pred = model.predict(X_val)
>>> skplt.metrics.plot_residuals_distribution(
>>>     y_val, y_val_pred, dist_type='tweedie',
>>> );

(Source code, png)

Residuals Distribution