tweedie

scikitplot._tweedie.tweedie = <scikitplot._tweedie._tweedie_dist.tweedie_gen object>

An instance of tweedie_gen, providing Tweedie distribution functionality.

This instance provides:

• probability density function (pdf)

• cumulative distribution function (cdf)

• random sampling

for the Tweedie distribution.

The Tweedie distribution is part of the exponential dispersion family, characterized by a p parameter that determines its behavior:

• p = 0: Gaussian distribution

• p = 1: Poisson distribution

• p = 2: Gamma distribution

• p = 3: Inverse Gaussian distribution

• 1 < p < 2: Compound Poisson-Gamma distribution

Parameters:

pfloat

Tweedie power parameter.

mufloat

Mean or location parameter.

phifloat

Dispersion parameter, controlling the variance of the distribution.

See also

tweedie_gen

A Tweedie continuous random variable.

Examples

Compute the pdf and cdf at a given point:

>>> import numpy as np
>>> from scikitplot.stats import tweedie
>>> x = 2.0
>>> pdf_val = tweedie.pdf(x, p=1.5, mu=1, phi=1)
>>> cdf_val = tweedie.cdf(x, p=1.5, mu=1, phi=1)
>>> pdf_val, cdf_val

(np.float64(0.15640119832636348), np.float64(0.8519363569424107))

Generate random variates:

>>> import numpy as np
>>> from scikitplot.stats import tweedie
>>> rvs = tweedie.rvs(p=1.5, mu=1, phi=1, size=16)
>>> rvs

array([0.        , 0.        , 2.99605199, 0.21965859, 0.        ,
       1.26044714, 0.57581449, 0.        , 1.35143558, 0.87845605,
       0.16350124, 0.53845568, 0.49384513, 0.        , 1.09758695,
       1.08003262])

Plot the pdf over a range:

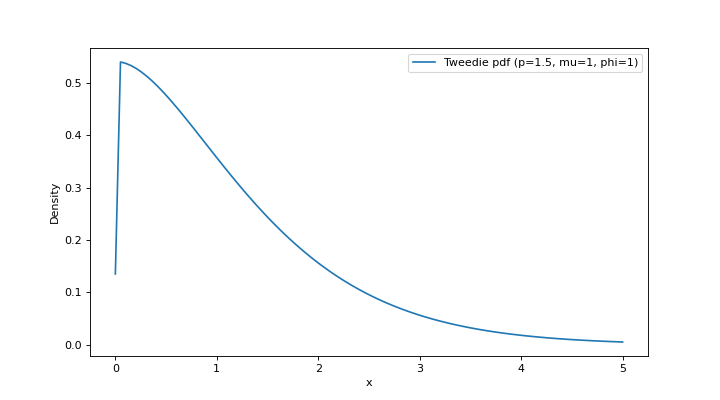
>>> import numpy as np
>>> from scikitplot.stats import tweedie
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 5, 100)
>>> y = tweedie.pdf(x, p=1.5, mu=1, phi=1)
>>> plt.plot(x, y, label='Tweedie pdf (p=1.5, mu=1, phi=1)')
>>> plt.xlabel("x")
>>> plt.ylabel("Density")
>>> plt.legend()
>>> plt.show()

(Source code, png)

Make live